MITARBEITER-HOMEPAGE

Prof. Dr.-Ing. Henry Graneß

Inhaber der Professur "Numerische Simulation im Maschinenbau" am Fachbereich Ingenieur- und Naturwissenschaften

Kurzvita:

2008-2013 Maschinenbaustudium an der TU Dresden mit Spezialisierung auf Entwicklung und Analyse von Antrieben sowie höhere Dynamik
2013-2018 Wissenschaftlicher Mitarbeiter an der TU Dresden; 2018 Promotion zum Thema „Raupenfahrzeug-Dynamik“
2013-2018 Freiberuflicher Berechnungsingenieur
2018-2021 Mitarbeiter bei Simpack (Dassault Systèmes), Schwerpunkte Mehrkörpersimulation, Kontaktmechanik, Antriebsdynamik
Seit 2021 Inhaber der Professur „Numerische Simulation im Maschinenbau“ an der TH Wildau

Lehre_{Bereich öffnen}_{Bereich schließen}

Sommersemester

Strömungslehre
Maschinenelemente II
Multiphysikalische Maschinen / Antriebsdynamik
Profilspezifisches Projekt

Wintersemester

Thermodynamik
Mechanische Verfahren (FEM)
Mehrkörpersimultion (MKS)
Numerische Mathematik

Projekte_{Bereich öffnen}_{Bereich schließen}

2023: Drehwegfehler von Verzahnungen
2020: Betriebsfestigkeit der Federgabel eines Mountainbikes (Machbarkeitsstudie)
2017 - 2018: Verzahnungsverschleiß von Wafer-Transportwagen
2016-2017: Analyse des Schwingungsveraltens eines Tagebauabsetzers, Optimierung der Seilanbindung der Abspannseile
2015: Schwingungsanalyse einer Mehrstufenwarmpresse, Nachrechnung der Lebensdauer von Schweißnähten
2015 - 2017: SRau-Dyn - Antriebssimulation Raupenfahrwerk

Bei Interesse an einer Forschungskooperationen sprechen Sie mich gern an.

Forschungsprofil und Dienstleistungen_{Bereich öffnen}_{Bereich schließen}

Analyse und Optimierung von Maschinen und Anlagen
Numerische Simulationsmethoden (insbesondere MKS & FEM)
Schwingungen in Antriebssystemen und Strukturen
Tragfähigkeit und Betriebsfestigkeit sowie beanspruchungsgerechtes Design von Maschinenelementen (Wellen, Lager, Verzahnungen)
Identifikation von Lastprofilen und Lastkollektiven (in Kombination mit experimentellen Methoden)
Optimierung von Antriebsregelungen, aktive und passive Schwingungsdämpfung
Strukturmechanik, Strukturdynamik
Kontaktmechanik
Erstellung von Berechnungsprogrammen für die eigenständige Nutzung im Betrieb

Veröffentlichungen_{Bereich öffnen}_{Bereich schließen}

Peer-Reviewed:

Graneß, H.: Methodik zur Analyse des Lagerringwanderns mithilfe von Ansatzvektoren. Forsch Ingenieurwes 88, 23 (2024). https://doi.org/10.1007/s10010-024-00738-2
Schulz, C.; Kieß, B.; Graneß, H.: Tooth root modeling induced variations of the calculated transmission error. NAFEMS World Congress: Tampa, 15th-18th May 2023
Graneß, H.; Schlecht, B.: Substitute Model for Crawler Track Units. ASME: 13th International Conference on Multibody Systems, Nonlinear Dynamics, and Control, 6.-9. August 2017, Cleveland (Ohio), USA
Schlecht, B.; Graneß, H.; Ulrich, C.: Time efficient simulation of drive trains. The 4th international Conference on Multibody System Dynamics 2016. 29. Mai – 02. Juni 2016, Montréal, Kanada
Schlecht, B.; Graneß, H.; Ulrich, C.: Freiheitsgradreduktion von MKS-Modellen der Antriebstechnik. In: antriebstechnik 12 (2015), S. 70-74
Schlecht, B.; Schulz, C.; Graneß, H.: Auswahlkriterium zur Bestimmung einer optimalen Schwingungsdämpfungsmaßnahme. In: antriebstechnik - antJournal 53 (2014) Nr. 3, S. 3-8

Weitere Veröffentlichungen:

Schlecht, B.; Graneß, H.; Mackel, J.: Comparison of drive shaft design concepts for rolling mill main drives. 30th European Plant Engineering Comittee (EPEC) 2014, Düsseldorf, 01./02. September 2014
Schlecht, B.; Graneß, H.; Schulz, C.: Vergleich von Kardangelenkwellen und Flachzapfenspindeln. AKIDA 2014, Aachen, 18./19. November 2014
Schlecht, B.; Schulz, C.; Graneß, H.: Die Mehrkörpersimulation als Grundlage der Systemanalyse. AKIDA 2014, Aachen, 18./19. November 2014
Schlecht, B.; Schulz, C.; Graneß, H.: Die Schädigungssumme als objektives Auswahlkriterium der Systemdynamik. SMK 2014, Rapperswil, 25./26. November 2014
Schlecht, B.; Graneß, H.; Mackel, J.: Vergleich von Antriebskonzepten für Walzgerüste. In: stahl und eisen 134 (2014) Nr. 12, S. 121-125
Schlecht, B.; Schulz, C.; Graneß, H.: Zur Bedeutung von Lasteingangsfunktionen. ATK 2015, Aachen, 03./04. März 2015
Schlecht, B.; Graneß, H.: Zur Schwingungsanalyse von Raupenfahrzeugen. Dresdner Maschinenelemente Kolloquium 2015, 8./9. Dezember 2015, Dresden
Schlecht, B.; Graneß, H.; Müller, F.: Dynamisches Verhalten von Raupenfahrwerks-Antrieben. Fachtagung Baumaschinentechnik 2015, 17./18. September 2015, Dresden
Schlecht, B.; Graneß, H.: Einfluss von Bauteilverschleiß auf die Antriebsdynamik von Raupenfahrwerken. AKAA 2016, 17. März 2016, Aalen
Schlecht, B.; Graneß, H.: Zur Modellfindung von Raupenfahrwerken. SMK 2016, 22./23. November 2016, Rapperswil, Schweiz
Schlecht, B.; Graneß, H.; Ramm, L.: Beanspruchungsminimierung in Raupenfahrwerksgetrieben. In: antriebstechnik 11 (2016), S. 140-145
Schlecht, B.; Graneß, H.: Methoden zur Analyse und Optimierung der Raupenfahrzeug-Dynamik. Dresdner Maschinenelemente Kolloquium 2017, 12./13. Dezember 2017, Dresden

Preise und Stipendien_{Bereich öffnen}_{Bereich schließen}

Enno-Heidebroek-Urkunde (2014)
ArcelorMittal - Studienförderung
3. Platz Innofab Ideenwettbewerb

Eigendynamik Turasantrieb

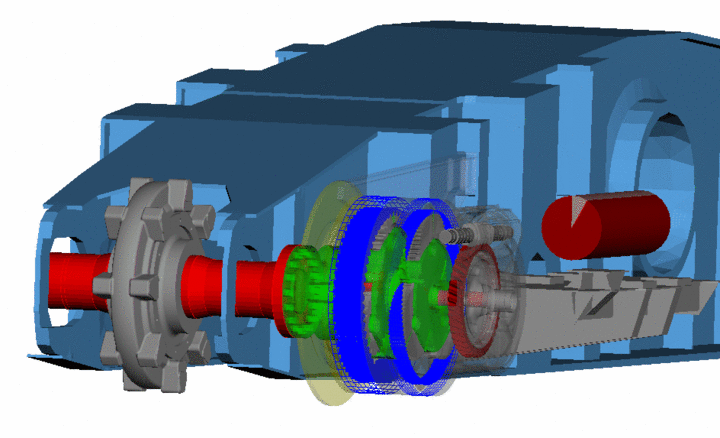
In dem Projekt "SRau-Dyn - Antriebssimulation Raupenfahrwerk" wurde die Fahrdynamik von Raupenfahrwerken großer Baumaschinen ganzheitlich analysiert und Strategien zur Minimierung der dynamischen Lasten sowie zur Steigerung der Bauteillebensdauer erarbeitet. Mithilfe der flexiblen Mehrkörpersimulation wurden dazu alle Komponenten der Baumaschine als mechanisches Modell abgebildet (Fahrwerk, Fahrwerksgetriebe, Oberbau) und zusammen mit der Fahrwerksregelung simuliert.

In der Animation ist die erste Torsionseigenform des Fahrwerkgetriebes dargestellt, welche neben den Fahrunruhen der Raupenkette einen entscheidenden Einfluss auf die Fahrdynamik hat. Hervorzuheben ist dabei, dass die Torsionsschwingung mit einer Biegeschwingung überlagert ist.

Betriebsfestigkeit Federgabel Mountainbike

In dieser Machbarkeitsstudie wurde untersucht, welche dynamischen Beanspruchungen in der Federgabel und dem Rahmen eines Mountainbikes entstehen. Unter Anwendungen der Struktur- und Mehrkörperdynamik erfolgte der Aufbau eines vollelastischen Mehrkörpersimulationsmodells, welches mit Eigenschwingungsanalysen sowie der Berechnung transienter Lasten Aussagen zu den schädigungsrelevanten Lastzuständen lierfert. Diese Lasten dienen im Nachgang dem FKM gestützten Betriebsfestigkeitsnachweis für die Federelemente der Gabel und der Schweißnähte des Rahmens.